Advice on selecting a camera – how many pixels?

You’re new to machine vision. You know you’ll need a camera and lens, but when you open the Edmund Optics catalog (or start surfing the web,) you’re overwhelmed by the options. So, in keeping with my mission of providing practical advice to machine vision users, here are a few tips:

The task dictates the hardware. Don’t buy a camera because you like the color, because there’s a pretty girl in the catalog or because it has more megapixels for the buck than any other camera. Start with the task.

Define the field of view – the area that you need to image. Don’t worry about fitting it to the proportions of the sensor (16:9, 4:3 or whatever,) just determine length and width, or diameter if that’s more appropriate. (Incidentally, I prefer to work in metric units – I just find it makes life easier.)

Now, a word of caution: Never plan on using every pixel in the sensor. This is because optical distortion and a fall-off in light intensity make the border pixels less reliable. To avoid using these I suggest adding 10% to the longest dimension you need to view, and calling that the field of view.

Now you need to determine the resolution required, in terms of pixels per millimeter. Okay, this can cause some head-scratching so let’s dive a little deeper.

The drivers for pixels per millimeter are either the smallest feature you need to detect, OR the required measurement resolution. If you need to check the presence of a screw in an assembly, then the smallest feature you need to find is that screw head. But how many pixels does it take to do that?

People have tried to apply some science to the business of how many pixels make a feature detectable but I prefer to rely on old-fashioned heuristics. (That’s “rule-of-thumb” to you!) The absolute minimum number of pixels needed to find a feature is a square measuring 3 pixels by 3. But, if it’s a circular feature you need to find this can result in only the center pixel fully covering the feature. The border pixels will have a grayscale value partway between that of the feature and the background, making detectability difficult. Thus 4 by 4 pixels is better and 5 by 5 better still.

Now, how about measurement resolution? Without going in to how an edge is detected, let’s just say that calculation of edge location depends on the gray levels of the surrounding pixels. And you can’t assume that the edge lines up neatly with the pixels; you’ll never have a white pixel adjacent to a black pixel – there will always be one or two shades of gray in between. So my heuristic for edge detection is that the uncertainty in the measurement will always be 3 pixels.

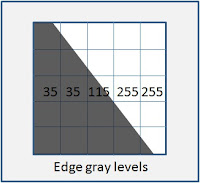But before you apply that to the tolerance on the part print, remember this: you almost certainly have two edges to find in your image, so the total uncertainty is 6 pixels, not 3. And how is this related to the part tolerance? Well opinions vary, but I suggest that the measurement uncertainty should be no more than 10% of the tolerance on the dimension. So if you’re measuring a feature that should be 25mm +/- 0.6mm, (I picked those numbers to make the arithmetic easier,) the uncertainty should be 0.060mm, meaning that you’ll want each pixel to span 0.010mm.

 

And with that number, you can calculate how many pixels are needed to image your field of view.